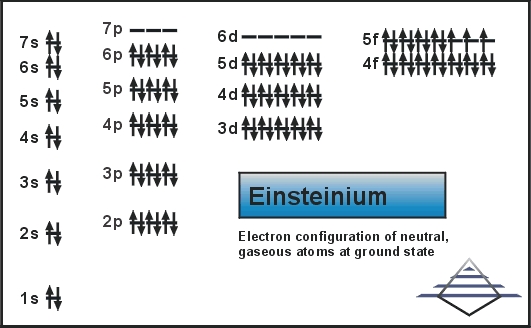
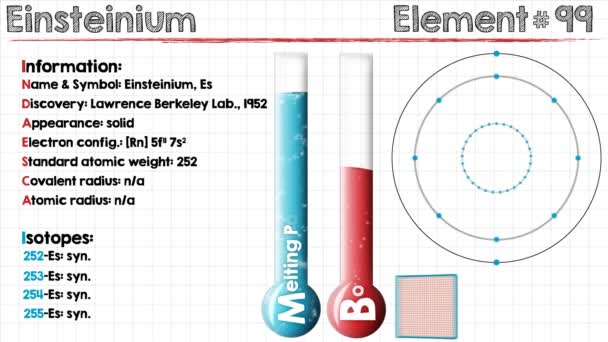
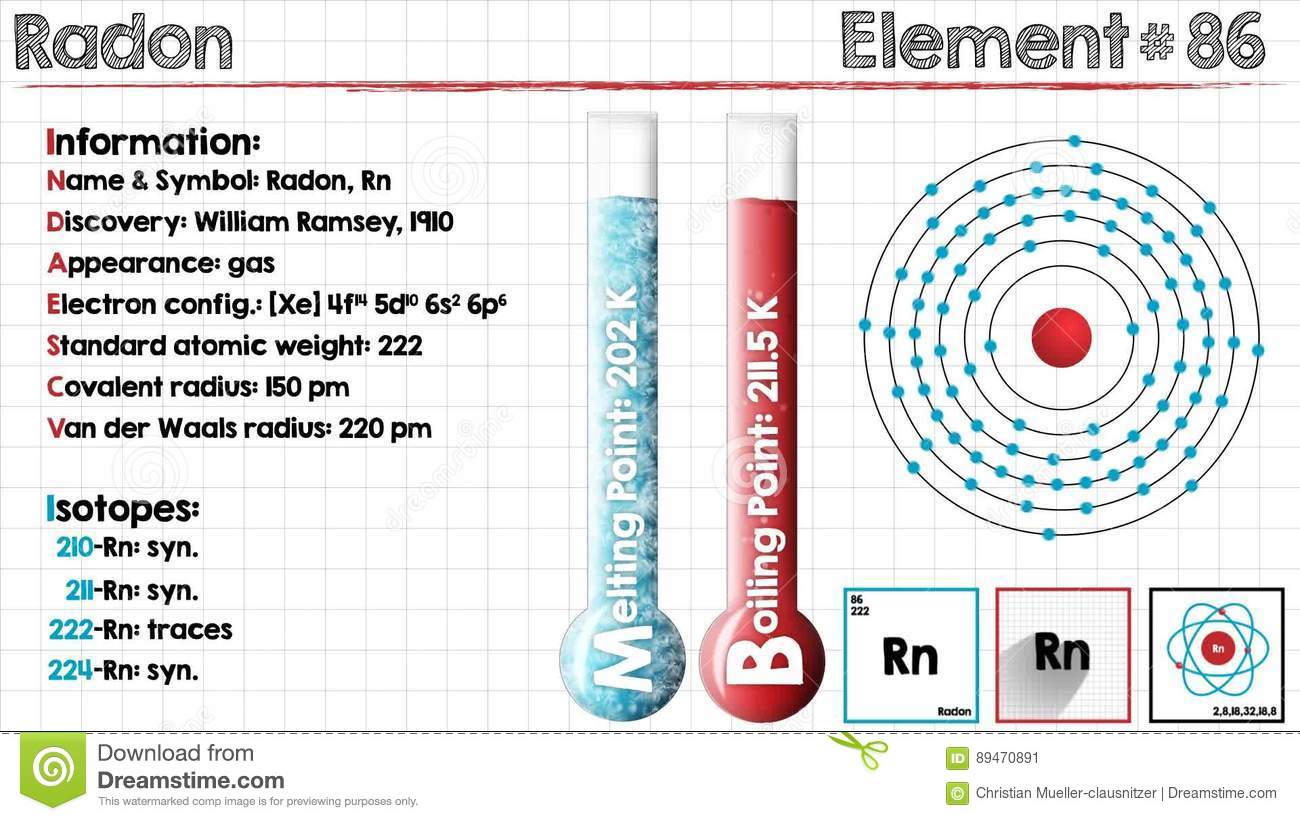
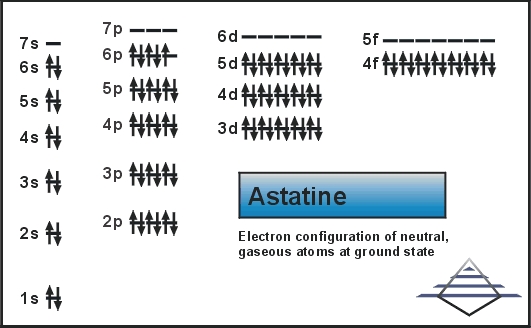
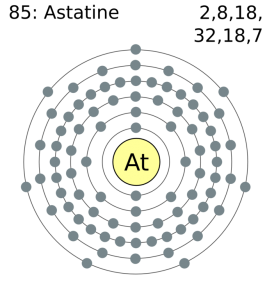
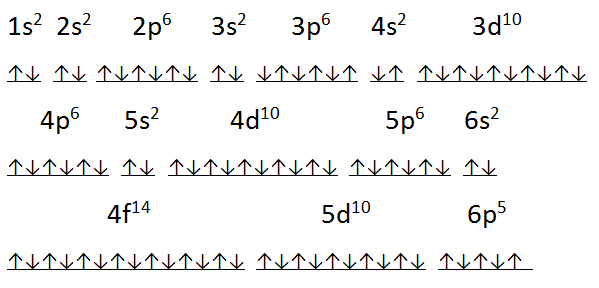
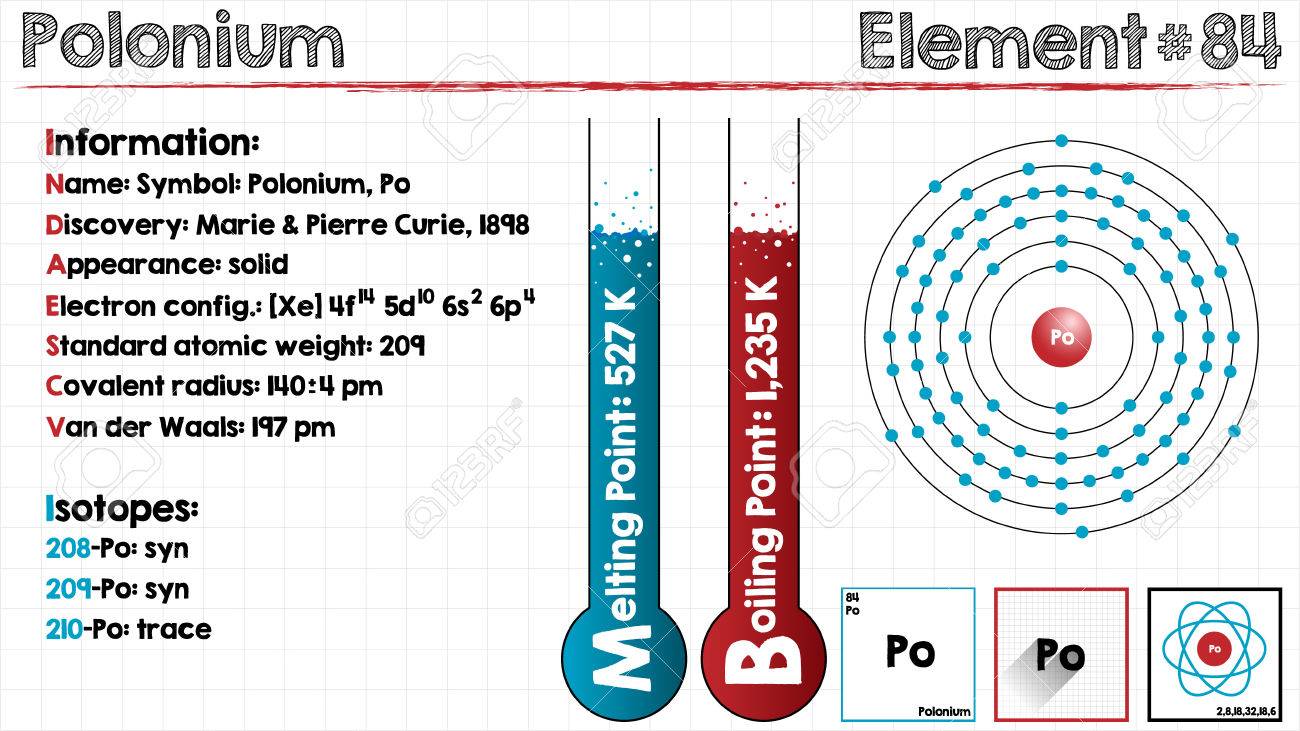
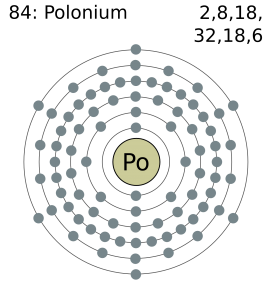
Electron Configuration For Einsteinium: Einsteinium is a synthetic chemical element which has a chemical symbol Es. The atomic number of Einsteinium is 99. As a member of the actinide series, Einsteinium is the seventh transuranic element. It was discovered in 1952 as the component of debris of the first hydrogen bomb explosion and was named after Albert Einstein.
It is a silvery, soft, paramagnetic metal. Einsteinium chemistry is typical of the late actinides, the +2 oxidation state is also accessible, with a preponderance of the +3 oxidation state; especially in solids. The very highly radioactivity of einsteinium-253 makes a visible glow and rapidly damages its crystalline metal lattice with a released heat of approx 1000 watts per gram. There is a difficulty in studying its properties which is due to the decay of einsteinium-253’s to berkelium-249 and then to californium-249 at the rate of about 3% per day.
The einsteinium isotope with the longest half-life, einsteinium-252 will be more suitable for investigating the physical properties of the einsteinium, but it has been proved far more difficult to produce and is available only in very fewer quantities and not in bulk quantity. It is the element with the highest atomic number that has been observed in macroscopic quantities in its purest form.
Today we are here to provide you with the information about the electron configuration of the Einsteinium along with the pictures that will help you to understand in a much better way. If you are also here for getting the information about this element then you are in the right place. Please see the full post below.
What is the Electron Configuration of Einsteinium?
Rn 5f11 7s2 is the electron configuration of the Einsteinium.
How Many Valence Electrons Does Einsteinium Have
Einsteinium has thirteen valence electrons in its outer shell.
Einsteinium Number of Valence Electrons
There are thirteen valence electrons in the outer shell of the einsteinium.