Want to know How To Calculate Electron Mass and Charge? The mass of the electron is also called the mass of a stationary electron. Because of its relation to the Avogadro constant, it is the fundamental constant of physics and is also very important in chemistry. Since it determines the number of observed effects in atomic physics so there are potentially many ways to determine its mass with an experiment.
Earlier, the mass of the electron was determined directly by combining two measurements. Arthur Schuster in 1890 first estimated the mass-to-charge ratio of the electron by measuring the deflection of “cathode rays” by a known magnetic field in a cathode ray tube. It was before it was even known what cathode rays were. Seven years later J. J. Thomson showed that cathode rays consist of streams of particles and they are called electrons.
How To Calculate Electron Mass and Charge?
The electron is a fundamental subatomic particle that plays a crucial role in the structure of atoms and the behavior of matter. To calculate the mass and charge of an electron, we need to refer to established scientific constants and formulas.
The mass of an electron is approximately 9.109 x 10^-31 kilograms. This value is extremely small, which is why in everyday situations, we tend to use a different unit known as the atomic mass unit (u) to express the mass of an electron. One atomic mass unit is equal to 1/12th the mass of a carbon-12 atom, which is roughly 1.66054 x 10^-27 kilograms. Hence, the mass of an electron is approximately 0.00054858 atomic mass units.
Regarding the charge of an electron, it has a fundamental charge of -1.602 x 10^-19 coulombs. This value represents the elementary charge, and it is the smallest unit of electric charge that exists in nature. Electrons carry a negative charge, while their counterpart, protons, carry an equal but positive charge.
In summary, to calculate the mass and charge of an electron, we use the following values:
- Mass of an electron: Approximately 9.109 x 10^-31 kg or 0.00054858 atomic mass units.
- Charge of an electron: -1.602 x 10^-19 C (coulombs).
Learn What are the Difference Between Charge and Electron here.
Electron Mass Number
The mass number of an electron is a concept that can be easily misunderstood, as electrons are not found in the nucleus of an atom, unlike protons and neutrons. The mass number applies specifically to nucleons, which are particles present in the nucleus.
To clarify, the mass number is the sum of protons and neutrons in an atom’s nucleus. Since electrons do not reside in the nucleus and their mass is significantly smaller than that of protons and neutrons, they are not included in the mass number calculation.
For example, consider a carbon-12 atom. “12” represents its mass number, indicating the sum of protons and neutrons in its nucleus. Carbon-12 has 6 protons and 6 neutrons, while the number of electrons is also 6. However, when calculating the mass number, we only consider the nucleons, so the mass number remains 12.
In summary, the mass number a property associated with the nucleus of an atom and is the sum of protons and neutrons. Electrons, being present in electron shells outside the nucleus, do not contribute to the mass number.
Electron Charge to Mass Ratio
The electron charge-to-mass ratio is a fundamental constant that has played a significant role in the development of modern physics. It sdenoted by the symbol “e/m” and represents the ratio of the electron’s charge (e) to its mass (m).
The value of the charge-to-mass ratio of an electron was first measured by J.J. Thomson in 1897 using cathode ray tubes. He observed the deflection of electrons in the presence of electric and magnetic fields and determined that the charge-to-mass ratio of an electron is approximately 1.75882 x 10^11 coulombs per kilogram (C/kg).
This value is of great importance as it allows scientists to predict the behavior of electrons in various electromagnetic fields. It is crucial in understanding the principles of particle accelerators, mass spectrometry, and even in the development of cathode ray tube televisions.
Moreover, the electron charge-to-mass ratio played a vital role in the discovery of the electron’s actual charge and mass. By comparing this ratio with the known elementary charge (e) and the mass of an electron (m), physicists were able to determine both the charge and mass independently.
Proton Neutron Electron Mass
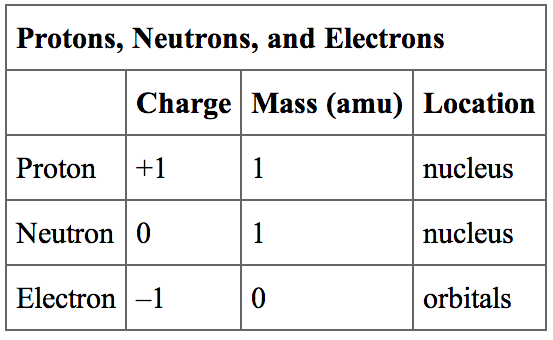
The proton, neutron, and electron are the three main subatomic particles that constitute atoms. Each of these particles has its own distinct mass, and together, they contribute to the overall mass of an atom.
The mass of a proton is approximately 1.6726219 x 10^-27 kilograms, which is about 1836 times the mass of an electron. Protons positively charged particles found in the nucleus of an atom. They play a vital role in determining the element’s identity as the number of protons defines the atomic number of an element.
On the other hand, the neutron is electrically neutral and also located in the nucleus. It has a slightly larger mass than the proton, with a value of approximately 1.6749275 x 10^-27 kilograms. The neutron’s presence stabilizes the nucleus by counteracting the electrostatic repulsion between protons.
The electron, as previously discussed, is much lighter than protons and neutrons, with a mass of approximately 9.109 x 10^-31 kilograms. Electrons negatively charged particles that orbit around the nucleus in specific energy levels or electron shells.
In summary, the masses of the subatomic particles are as follows:
-
- Proton mass: Approximately 1.6726219 x 10^-27 kg.
- Neutron mass: Approximately 1.6749275 x 10^-27 kg.
- Electron mass: Approximately 9.109 x 10^-31 kg.
Mass of Electron in Grams
The mass of an electron is an exceedingly small value, and expressing it in grams results in an even more minuscule number. However, it is still an interesting exercise to do so.
The mass of an electron is approximately 9.109 x 10^-31 kilograms, as we discussed earlier. To convert this mass into grams, we need to know that 1 kilogram is equal to 1000 grams. Therefore, to express the electron’s mass in grams, we perform the following calculation:
Mass of electron in grams = 9.109 x 10^-31 kg * (1 kg / 1000 g)
Mass of electron in grams ≈ 9.109 x 10^-34 grams
As you can see, the mass of an electron in grams is an extremely tiny value, approximately 9.109 x 10^-34 grams. Such a small mass is characteristic of subatomic particles and is one of the reasons why atomic and quantum physics operate on such different scales compared to everyday experiences.
It is essential to remember that the gram is a unit of mass used for everyday objects, and the realm of subatomic particles requires more specialized units, such as kilograms or atomic mass units, to express their masses more conveniently.