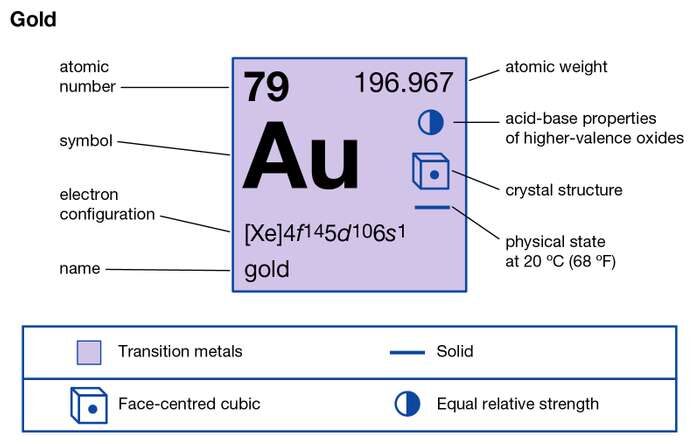
Know and study the Gold valence electrons here for the thorough knowledge of this element. We are further going to provide every possible information about the element. Gold is a globally recognized and valued chemical element. It is represented by the symbol Au with its atomic number 79.
How many valence electrons does Gold have?
Gold has its natural form in the crust of the earth. It’s one of those chemical elements which have higher atomic numbers with their natural occurrence. Gold appears like a soft yellowish and dense chemical element. It falls in the category of group 11 transition metals and has the very least reactive properties.
Gold basically occurs in its natural form within the rocks, alluvial deposits or veins. It has a solid solution form along with the other metals such as silver, copper etc. Gold is undoubtedly one of the high value carrying chemical elements. It has significant importance around the world for various usages.
The chemical element has a history of its importance in various forms. For example, gold may take the shape of precious jewelry, coins, or other artistic stuff. Nearly 50% of the world’s gold has the form of Jewelry which clearly states its importance. The rest of 50% has the form of investment and another industrial usage.
China has the maximum production of gold in its reserves or stored under the ground. Australia and Russia are the other nations to have a significant amount of gold.
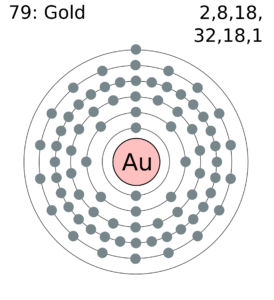
Gold Valence Electrons Dot Diagram
You can study the electron valence of Gold with better insight by using the dot diagram of elements. The diagram will help in understanding the chemical binding of valence electrons.
It will further provide the accurate numbers of valence electrons of atoms. The interaction of valence electrons helps in understanding the chemical binding of elements.
Valency of Gold
The valency of gold may be either of 1 or 3 in different scenarios. It is the transition metal due to which it has the variable valency.
So, the most typical valency of gold remains 3. There may further be some occasional scenario when the gold may have valency as 3.
Leave a Reply